Latent generative models have emerged as a leading approach for high-quality image synthesis.
These models rely on an autoencoder to compress images into a latent space, followed by a generative
model to learn the latent distribution. We identify that existing autoencoders lack equivariance
to semantic-preserving transformations like scaling and rotation, resulting in complex latent spaces
that hinder generative performance.
To address this, we propose EQ-VAE, a simple regularization approach
that enforces equivariance in the latent space, reducing its complexity without degrading reconstruction
quality. By fine-tuning pre-trained autoencoders with EQ-VAE, we enhance the
performance of several state-of-the-art generative models, including DiT, SiT,
REPA, and MaskGIT, achieving a ×7 speedup on
DiT-XL/2 with only five epochs of SD-VAE fine-tuning.
EQ-VAE is compatible with both continuous and discrete autoencoders,
thus offering a versatile enhancement for a wide range of latent generative models.
Motivation
Our work is motivated by a key observation: state-of-the-art autoencoders,
such as SD-VAE, produce latent representations
that are not equivariant under basic spatial transformations
like scaling and rotation. To test this, we applied scaling and rotations directly
to the latent code and evaluated the corresponding reconstructions. While
autoencoders reconstruct images accurately when transformations are applied
to the input (i.e., \( \mathcal{D}(\mathcal{E}(\mathbf{\tau} \circ \mathbf{x})) \)),
applying transformations directly to the latent representation
(i.e., \( \mathcal{D}(\mathbf{\tau} \circ \mathcal{E}(\mathbf{x})) \)) leads
to significant degradation in reconstruction quality:
Equivariance Regularization: To overcome this limitation, we propose a regularization objective that aligns the reconstructions of transformed latent representations (\(\mathcal{D}\big( \tau \circ \mathcal{E}(\mathbf{x}) \big)\)) with the corresponding transformed inputs (\(\tau \circ \mathbf{x}\)). Specifically, we modify the original training objective of \(\mathcal{L}_{\text{VAE}}\) as follows:
\[ \begin{aligned} \mathcal{L}_{\text{EQ-VAE}} (\mathbf{x}, \textcolor[RGB]{225,0,100}{\tau}) &= \mathcal{L}_{rec}\Big( \textcolor[RGB]{225,0,100}{\mathbf{\tau} \circ} \mathbf{x},\, \mathcal{D}\bigl( \textcolor[RGB]{225,0,100}{\mathbf{\tau} \circ}\mathcal{E}(\mathbf{x}) \bigr) \Big) + \lambda_{gan}\,\mathcal{L}_{gan}\Big( \mathcal{D}\bigl( \textcolor[RGB]{225,0,100}{\mathbf{\tau} \circ}\mathcal{E}(\mathbf{x}) \bigr) \Big) + \lambda_{reg}\,\mathcal{L}_{reg} \notag \end{aligned} \] Notice that when \(\textcolor[RGB]{225,0,100}{\mathbf{\tau} }\) is the identity transformation, this formulation reduces to the original objective of SD-VAE
We focus on two types of spatial transformations: anisotropic scaling and rotations . These are parameterized as:
\[
\mathbf{S}(s_x, s_y) =
\begin{bmatrix}
s_x & 0 \\
0 & s_y
\end{bmatrix}
,\quad
\mathbf{R}(\theta)=
\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}
\]
The final transformation is the composition of scaling and rotation:
\(\tau = \mathbf{S}(s_x, s_y) \cdot \mathbf{R}(\theta)\).
We sample uniformly \(0.25 < s_x, s_y < 1\), and
\(\theta \in \left(\frac{\pi}{2}, \pi, \tfrac{3\pi}{2}\right)\).
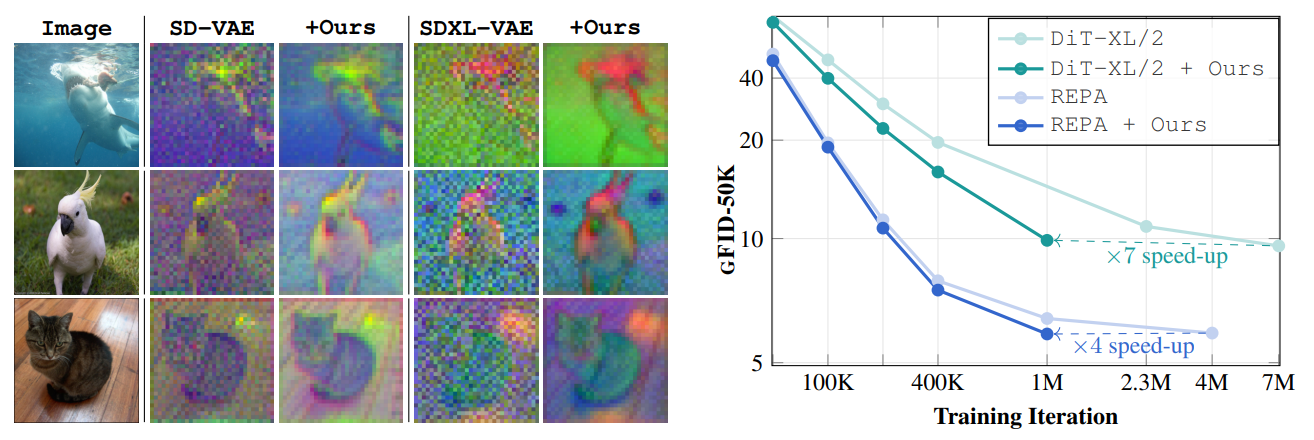
We demontrate images generated by two DiT-XL/2 models for
50K 100K and 400K iterations, one trained on the latent
distribution of the standard SD-VAE and
one on our regularized EQ-VAE.
Both models share the same noise and number of sampling steps.
The model trained on EQ-VAE is significantly speed-up.
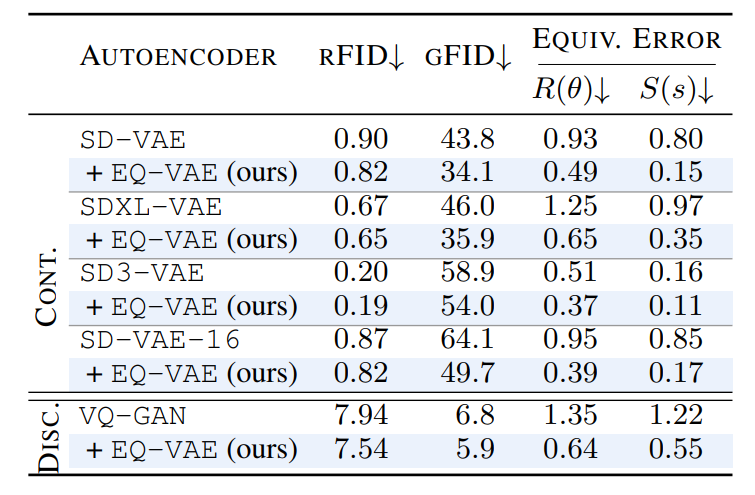
(Table Left) Our regularization seamlessly adapts to both continuous and discrete autoencoders. Finetuning
pretrained autoencoders with EQ-VAE reduces the equivariance error under spatal transformations
resulting in enhancement in generetaive performance (gFID) while maintaining the prior reconstruction capabilities (rFID).
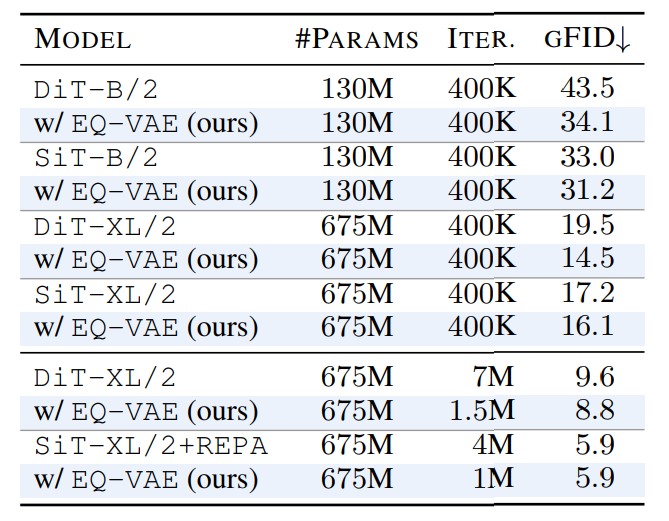
(Table Right) State-of-the-art diffusion transormer models experience significant perfmance boost when
trained on the latent representations on EQ-VAE
How fast is EQ-VAE regularization?
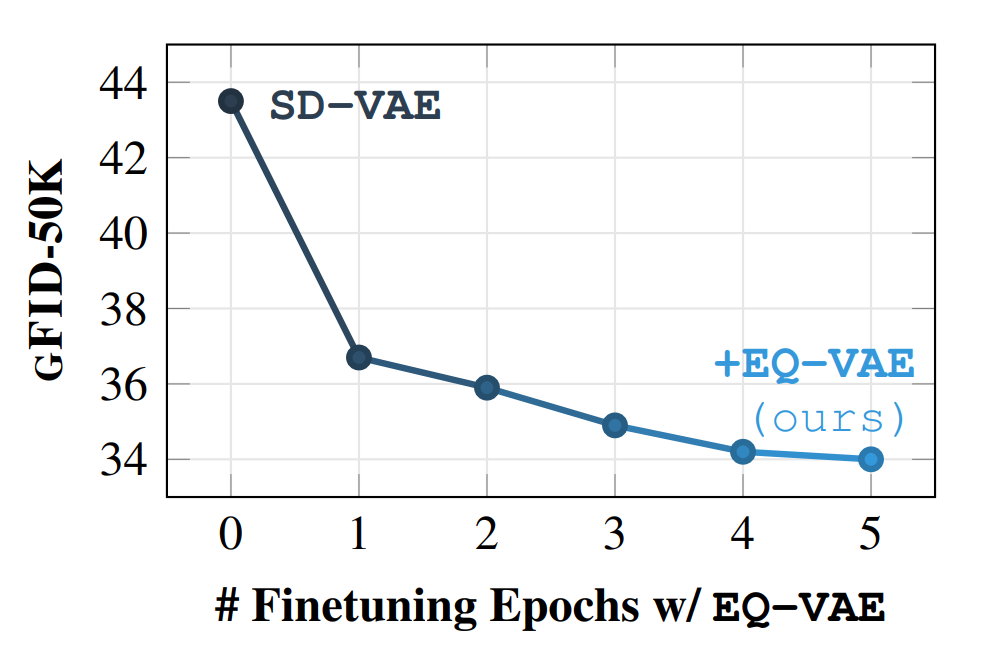
We train a
DiT-B/2 model on the resulting latent distribution of each
epoch and present the results in
Even
with a few epochs of fine-tuning with EQ-VAE, the gFID
drops significantly, highlighting the rapid refinement
our objective achieves in the latent manifold.
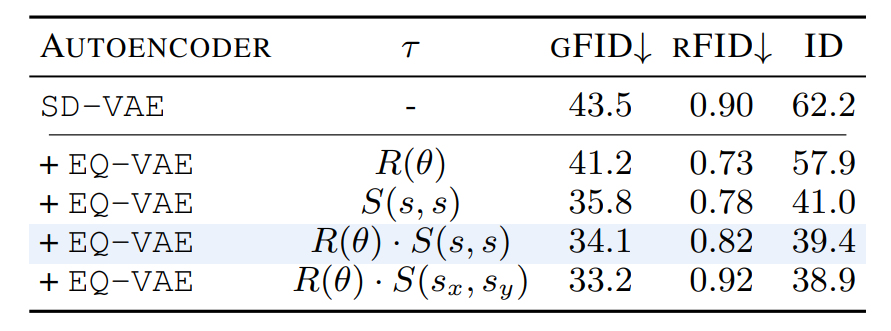Latent space complexity and generative performance. We observe a correlation be-
tween the intrinsic dimension (ID) of the latent manifold and
the resulting generative performance. This suggests that the
regularized latent becomes simpler to model.
@inproceedings{eqvae,
title = {EQ-VAE: Equivariance Regularized Latent Space for
Improved Generative Image Modeling},
author = {Kouzelis, Theodoros and Kakogeorgiou, Ioannis and Gidaris, Spyros and Komodakis, Nikos},
booktitle = {arxiv},
year = {2025},
}